How to calculate an angle
You can use pattern-spotting, logic and reasoning to work out angles around straight lines.
Some facts that are useful to remember are:
- 360° is a full turn
- 180° is half a turn
Angles on a straight line
Did you know that one half turn is 180°?
If the straight line or half turn is divided into two angles, and we know one of the angles, we can work out the other.
Here 120° + 60° = 180°
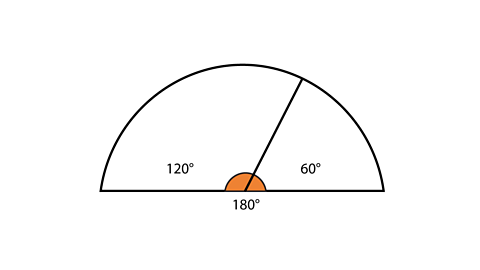
If we just had information on one of the angles e.g. 120°, we could work out the other angle is 60°.
If the straight line was divided into three angles, all three angles would add up to 180°.
Here are some more examples of angles on straight lines, can you see how they all add up to 180°?
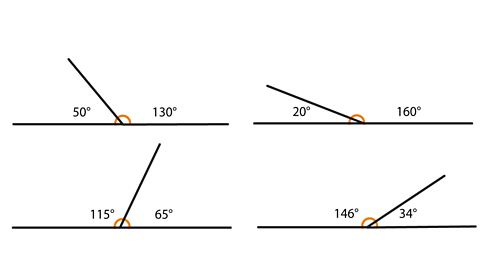
Example 1
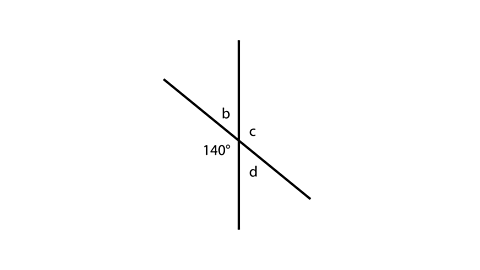
Can you work out what angle b is?
b is on a straight line with 140°, so must be 40°.
140° + 40°= 180°
What about angle c?
b + c = 180°, so if b is 40°, c must be 140°.
40° + 140° = 180°
Angle d must be 40° as it is on a straight line with c.
c+ d = 180°

Vertically opposite angles
Vertically opposite angles are the angles directly opposite each other when a straight line crosses over another straight line.
They are always equal.
What do you think angle c is in both of these diagrams?
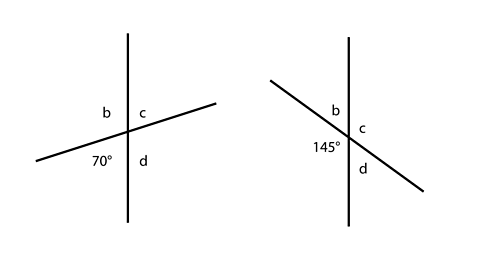
In the first diagram angle c equals 70° and in the second diagram angle c equals 145°.
Angles b and d are vertically opposite, so they are equal too.

Remember
- Angles on a straight line add up to 180°.
- When two straight lines cross, vertically opposite angles are always equal.

Activities
Quiz 1
Quiz 2
Take this quiz to practise solving problems with angles.
NEW! Play Guardians: Defenders of Mathematica - the winter update. gameNEW! Play Guardians: Defenders of Mathematica - the winter update
It's Mathematica as you’ve never seen it before, with all-new festive backgrounds and costumes. Available for a limited time only. Use your maths skills to save the day before it's too late!

More on Lines and angles
Find out more by working through a topic
- count8 of 10

- count9 of 10

- count10 of 10

- count1 of 10
