91�ȱ�

Polygons are 2D shapes that have straight sides. Regular polygons have sides and angles that are all the same size.

Let's recap what a polygon is with this quick video.

How would you work out the sum of internal angles in a polygon that has more than 4 sides?

There is a formula that you can use to work out the sum of internal angles that works for all polygons:

Sum of internal angles= (number of sides - 2) x 180°

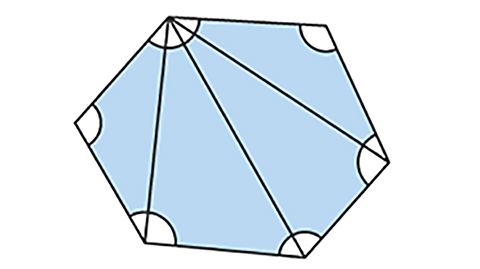
Did you know that once you have subtracted 2 from the number of sides, this actually represents the amount of triangles that the polygon is able to be partitioned into from the same vertex?

That’s why you then multiply by 180° - that’s the sum of the internal angles within a triangle.

Here's how you would change the formula for the different polygons below.

You can even try drawing the shapes out yourself and practise partitioning them into the correct amount of triangles.

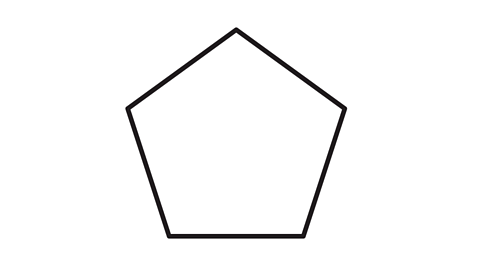
Any pentagon has 5 sides. Use the formula to work out what the internal angles total:

sum of internal angles = (5 - 2) x 180°

540° = 3 x 180°

What would one angle be worth in a regular pentagon?

Just divide 540 by the number of angles there are:

540° ÷ 5 = 108°

Since a hexagon has 6 sides, let’s substitute that amount into the formula:

sum of internal angles = (6 - 2) x 180
720° = 4 x 180

What would one angle be in a regular hexagon?

720° ÷ 6 = 120°

All heptagons have 7 sides, so the formula to work out the internal angles would be:

sum of internal angles = (7 - 2) x 180
900° = 5 x 180°

What would one angle in a regular heptagon be?

900° ÷ 7 = 128. 57° (rounded to 2 decimal places)

Octagons have 8 sides so again, we need to adjust the formula accordingly:

sum of internal angles = (8 - 2) x 180°
1080° = 6 x 180°

In a regular octagon, one angle would be worth:

1080° ÷ 8 = 135°

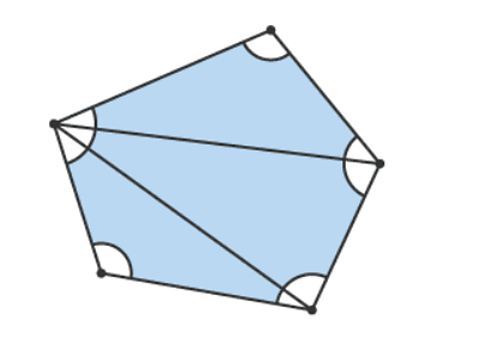
In irregular polygons, like this one above, the sum of the interior angles would always be the same, but the value of an individual angles wouldn’t be since they are different sizes!

Put your knowledge of interior angles of polygons to the test in this quick quiz.

Now have a go at this quiz and try to find the missing angles in the quadrilaterals and regular polygons.