Key points
- A sequenceA sequence is a set of numbers that follow a certain rule. For example, 3, 5, 7, 9… is a sequence starting with 3 and increasing by 2 each time. is a list of numbers or diagrams that are in a particular order.
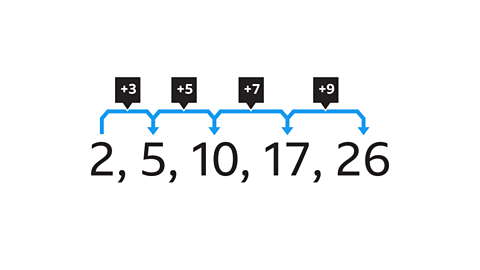
- For example, a number pattern which increases (or decreases) by the same amount each time is called an arithmetic sequenceAn arithmetic sequence is a sequence of numbers with a definite pattern. If you take any number in the sequence then subtract the previous one, the result is always a constant amount..
- The amount it increases or decreases by is known as the common difference.
- Recognising the common difference means that the sequence can be continued using a term-to-termA term-to-term rule is a rule that allows you to find the next number in a maths sequence, if you know the previous numbers (or terms). rule.
- The đť’Źth term refers to a term's position in the sequence, for example, the first term has đť’Ź = 1, the second term has đť’Ź = 2 and so on. An expression for the đť’Źth term is worked out by looking at the difference between the terms of the sequence and comparing the sequence to the appropriate times table.

Video
Watch the video to learn about arithmetic sequences and how any number in a sequence can be found using the \(n\)th term rule.
An arithmetic sequence is a series of numbers that go up or down by the same amount each time.
In the song Ten Green Bottles Standing on the Wall, the sequence goes ten, nine, eight, seven, six and so on, reducing by one each time. This is called the common difference. In this sequence the common difference is -1
A term-to-term rule can be created to explain the common difference. In the sequence 11, 14, 17, 20, 23, it's plus three because the sequence goes up by three with each term.
It might be necessary to work out a number much later in the sequence though. For example, what the 93rd number is and it would take ages to add three 92 times.
This is where the đť’Źth term rule comes in handy. The đť’Źth term is a way of using the position of a term in a sequence, to find out what that term would be. Since the common difference is three, start by comparing the sequence to the three times table. Subtracting the number in the times table from the term results in a constant difference of plus eight between the table and the sequence.
3 + 8 is 11, 6 + 8 is 14 and so on. To find the 93rd term multiply the common difference, 3 by 93, and then add 8 to get the answer, 287
The đť’Źth term rule can be expressed as 3đť’Ź + 8, with đť’Ź representing the term needing to be found.
Sequences come up all the time in real life, so the đť’Źth term rule can really come in handy.
How to find missing terms in an arithmetic sequence
To find the common difference, work out how much the terms are increasing or decreasing by from one term to the next.
- Subtract consecutiveone after the other pairs of numbers in the sequence.
- Once the common difference is identified, continue the sequence in the same pattern.
The common difference can be used to find the missing terms in a sequence.
Examples

Image caption, Look at the difference between each pair of terms in the sequence. This is found by subtracting the lowest term in the pair from the highest, for example 8 - 5 = 3
Image caption, 8 – 5 = 3, 11 – 8 = 3, 14 – 11 = 3. The common difference between terms is 3 and the term-to-term rule is +3
Image caption, The sequence will continue in the same way, adding 3 to the previous term.
Image caption, 14 + 3 = 17, 17 + 3 = 20 and 20 + 3 = 23 so as a result the next 3 terms are 17, 20 and 23
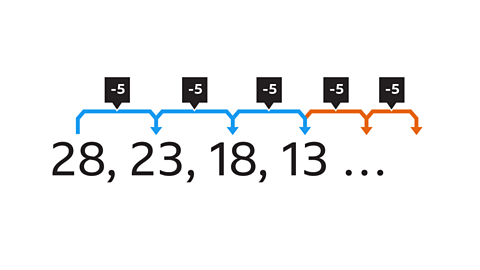
Image caption, What are the next two numbers in this sequence?
Image caption, This time, the numbers in the sequence are decreasing, with each term being 5 less than the previous term, so the term-to-term rule is -5
Image caption, The sequence will then continue in the same way, subtracting 5 from each previous term.
Image caption, The next two terms are 8 and 3, as 13 – 5 = 8 and 8 – 5 = 3
1 of 9
Question
What are the next two numbers in this arithmetic sequence?

The common difference is 6 between each pair of terms. Eg, the difference between 2 and 8 is 6
The next two terms in the sequence are found by adding 6 to the previous terms:
20 + 6 = 26 and 26 + 6 = 32
The common difference is 6 between each pair of terms, so the next two terms in the sequence are 26 and 32

The đť’Źth term of an arithmetic sequence
Rather than finding the next term or next two terms of a sequence, it may be necessary to work out the 10th or the 100th term, for example.
Writing out 100 terms would take time and mistakes could be made when recording all the numbers.
Instead, a simpler calculation can be used, as well as a general rule called the '\(n\)th' term.
The \(n\)th term is a formula which means that any number in the sequence can be calculated without having to write the whole sequence out.
Examples

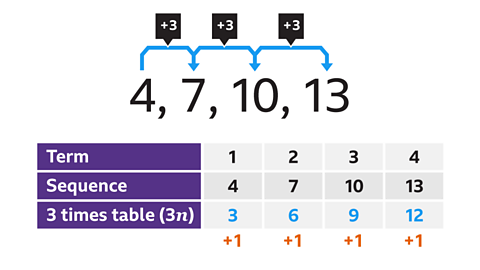
Image caption, Find the đť’Źth term and the 100th term in this sequence.
Image caption, The common difference between each pair of terms is 3. As a result, the đť’Źth term for this sequence is related to the 3 times table.
Image caption, The sequence 3, 6, 9, 12, 15 follows the 3 times table. Multiplying the term number by 3 gives the corresponding term in the 3 times table: 1 x 3 = 3, 2 x 3 = 6, 3 x 3 = 9, 4 x 3 = 12, 5 x 3 = 15
Image caption, Following this rule, the đť’Źth term is 3 x đť’Ź or 3đť’Ź. The 100th term in this sequence would be 3 x 100 = 300. If you wanted to work out a different number within the sequence, then simply multiply the term number by 3. Eg, the 20th term would be 3 x 20 = 60
Image caption, Find the đť’Źth term in this more complex sequence.
Image caption, The common difference between each pair of terms is 5. This means that the đť’Źth term for this sequence is related to the 5 times table. However, this sequence is different to the sequence of numbers in the 5 times table.
Image caption, The common difference between terms in the sequence is 5. Write the 5 times table (5đť’Ź) directly beneath the sequence of numbers that are given.
Image caption, Compare the sequence with the numbers in the 5 times table. Subtract the number in the 5 times table from the number in the sequence. This gives a constant difference of +2. For example, 7 – 5 = 2, 12 -10 = 2, and 17 – 15 = 2. The general rule for the 𝒏th term is 5𝒏 + 2
Image caption, The đť’Źth term of this sequence is 5đť’Ź + 2. Using this general rule it is possible to find any term within the sequence without writing down each number. Eg, to find the 20th term use đť’Ź = 20 in the rule for the đť’Źth term, 5đť’Ź + 2 = 5 x 20 + 2, so 100 + 2 = 102. The 20th term in this sequence would be 102
1 of 9
Question
What is the \(n\)th term of the following sequence?

The common difference between each pair of terms is 3. The sequence is linked to the 3 times table (3\(n\)).
- Write the 3 times table below the sequence in a table.
- Compare the two sequences by subtracting the matching terms in the given sequence with numbers in the 3 times table. This gives a constant difference of +1
Eg:
4 – 3 = 1
7 - 6 = 1
10 – 9 = 1
etc.
The \(n\)th term is 3\(n\) + 1
Practise arithmetic sequences
Quiz
Practise using arithmetic sequences and finding the \(n\)th term with this quiz. You may need a pen and paper to help you with your answers.
Real-life maths

Sequences can be used in everyday life.
For example, a farmer may use sequences when buying fence rails for his land. There is a connection between the number of posts and the number of fence rails required.
| posts | rails |
|---|---|
| 1 | 0 |
| 2 | 3 |
| 3 | 6 |
| 4 | 9 |
The 𝒏th term for this sequence would be 3𝒏 – 3 (where 𝒏 is the number of posts.)If the farmer needs 50 posts (spread 1 m apart) then they would require:(3 x 50) – 3= 150 – 3= 147 fence rails.
If the farmer had a larger field and needs 100 posts (spread 1 m apart) then they would require:(3 x 100) – 3= 300 – 3= 297 fence rails.

Game - Divided Islands
Play the Divided Islands game! gamePlay the Divided Islands game!
Using your maths skills, help to build bridges and bring light back to the islands in this free game from 91Čȱ¬ Bitesize.

More on Patterns and sequences
Find out more by working through a topic
- count3 of 4
- count4 of 4