91�ȱ�

Sometimes in mathematics we like to use letters to represent numbers.

The ‘value’ of these letters can change according to certain rules or conditions we are given – hence we can call them variables.

What is the value of A?

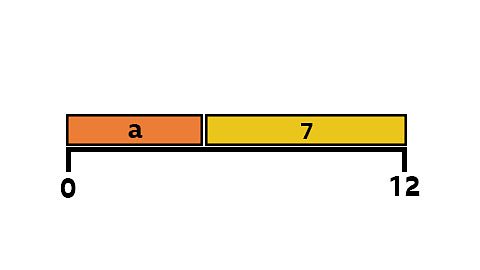
What number do we have to add to 7 to make 12?

What is the value of the unknown to make both sides of this equation balance?

a + 7 = 12

There is only one answer to the value of the letter a. No other values of a will make the equation balance!

To find a, you can subtract 7 from 12.

12 - 7 = 5

The answer is: a = 5

Here is an equation with two variables (or unknowns):

b + c = 12

Can you find two numbers that add together to make 12?

There is certainly more than one answer this time – why? There are many, many possibilities!

Here are some examples:

b = 5, c = 7

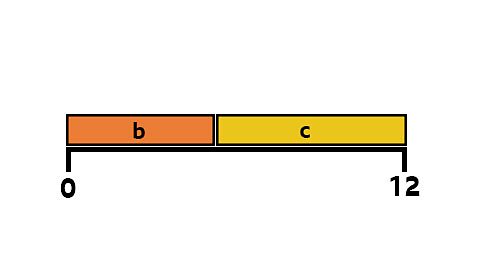
b = 8, c = 4

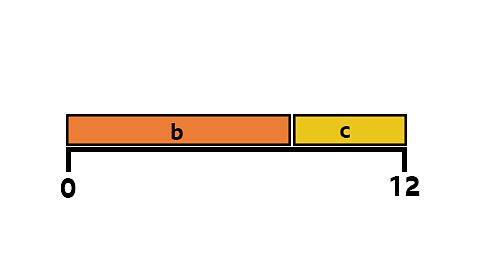
b = 2, c = 10

We could use a table to start listing some of the possible combinations of the letters b and c:

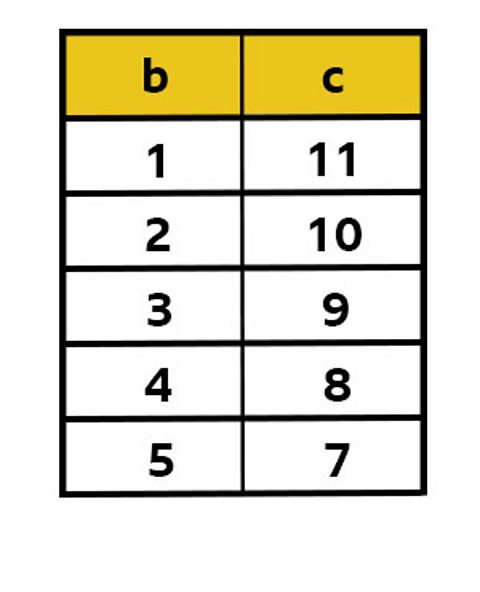
…and so on.

What about if b = 2½ and c = 9½ ?

What about b = 4.7 and c = 7.3 ?

What about b = 14 and c = -2 ?

Wow! There are endless possibilities.

We say there are an infinite number of possibilities or solutions to this equation with two variables.

What difference would it make if we said that the values of b and c had both to be positive whole numbers?

Here is another equation with two variables (or unknowns)

d + e = 18

In this equation, though, we are also told that the value of d is twice the value of e.

The answer is:

d = 12, e = 6

There is only one pair of answers to d and e because the value of d has to be twice the value of e.

No other values of d and e will make the equation balance given the additional information we have been given!

Jasmine has some 20p and 50p coins.

Altogether she has £2.40

How many of each coin could she have?

Jasmine decides to displays her answers in a table:

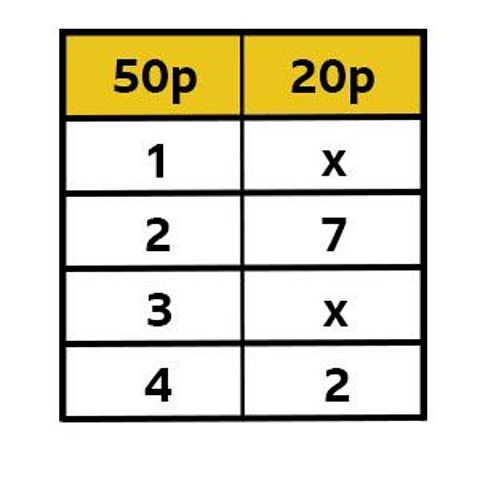
The table allows her to be able to check that she has all the possible answers!

Can you explain each line of the table? What does the ‘x’ represent?

This is another example of a problem with two unknowns – how many 50p coins and how many 20p coins to have a given total.

Clearly there is not an infinite number of solutions as we saw in Example 2.

In fact there are just two possible solutions:

(2 x 50p) + (7 x 20p)

and

(4 x 50p) + (2 x 20p)