91�ȱ�

Translations and reflections are examples of transformations.

A transformation is a way of changing the position (and sometimes the size) of a shape.

Look at the grid below, which is an example of one we can use to describe this movement.

The picture shows a pair of axes, dividing a grid into four quadrants.

The horizontal, or x axis is numbered from -5 to 5.

The vertical, or y axis is also numbered from -5 to 5.

The two axes intersect at right angles at the point we call the origin.

In geometry, the word translation simply means moving.

When we translate a shape every point on the shape moves the same distance and in the same direction.

Translating a shape will not change the size of the shape or rotate it. It will stay ‘the same way round’, or we could say that the orientation stays the same.

A simple example of a translation would be:

Move the shape 4 units to the right and 5 units down.

We might be asked to reflect a shape in a given mirror line. This line of reflection could be the x or y axis or a totally different line.

When a shape is reflected, an image of that shape is created. It is like ‘flipping’ the shape over the line of reflection.

We have to make sure that each point on the original shape is the same distance from the line of reflection as the corresponding point on the image.

Translations and reflections are examples of transformations where both the original shape and the resulting image are congruent, which means they have the same shape and size.

Let's look at the grid below.

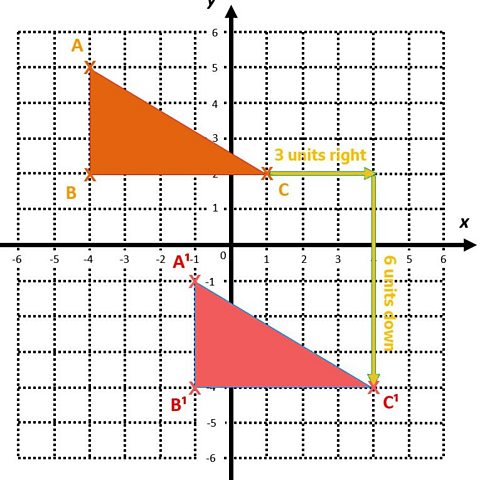
The right angled triangle ABC is positioned in the first and second quadrants.

The co-ordinates of the triangle are A(-4,5), B(-4,2) and C(1,2).

The triangle ABC is translated 3 units to the right (parallel to the x axis) and 6 units down (parallel to the y axis).

The resulting image of this translation has been labelled ��¹��¹��¹.

The diagram shows how the point C has moved but every point has moved the same distance and the same direction.

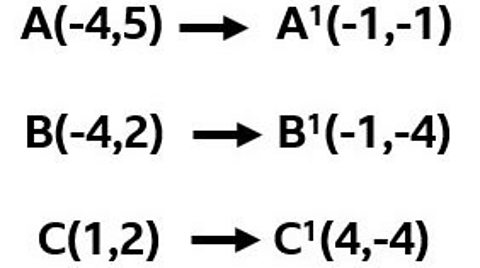
This means, as with all translations, that the original triangle ABC and its image ��¹��¹��¹ are the same size and shape.

The orientation following this transformation is unchanged.

The triangle ABC and the triangle ��¹��¹��¹ are congruent.

Now look at this next grid.

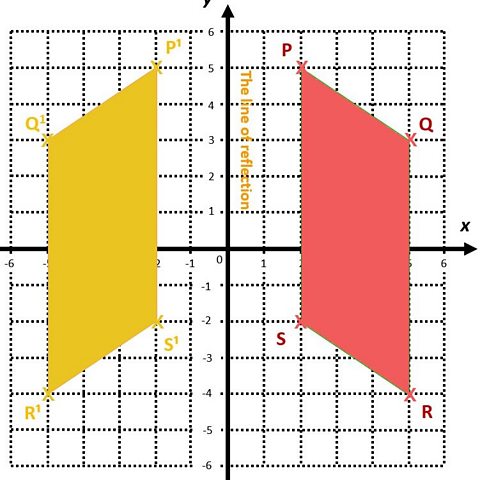
The parallelogram PQRS is positioned in the first and fourth quadrants.

The co-ordinates of the parallelogram are P(2,5), Q(5,3), R(5,-4) and S(2,-2).

The triangle PQRS has been reflected in the y axis (line of reflection).

The resulting image of this reflection has been labelled ��¹��¹��¹��¹.

Each point on the original shape is the same distance from the line of reflection as the corresponding point on the image.

The corresponding points are opposite one another following this ‘flip’.

The two parallelograms are the same size and shape.

However, this transformation has changed the orientation of the original shape.

The parallelogram PQRS and the parallelogram ��¹��¹��¹��¹ are congruent.

Look at this final grid.

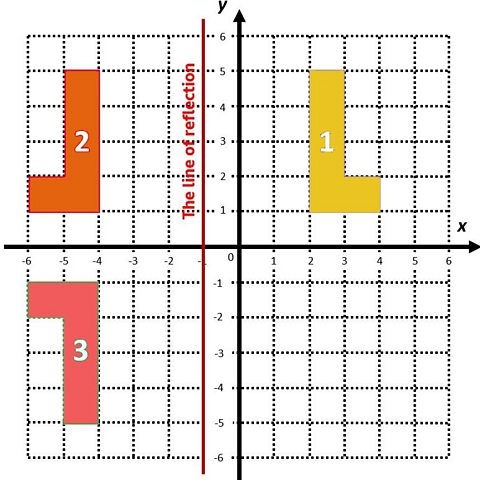
The L shape (irregular hexagon) labelled 1 is positioned in the first quadrant.

This shape is then reflected in a line that is parallel to the y axis.

This line of reflection is called the line x=-1

This is because the x coordinate of every point on the line will always be -1.

The resulting image has been labelled 2.

Now another reflection!

The L shape labelled 2 is now reflected in the x axis.

The resulting image has been labelled 3.

All three L shapes are the same shape and size and therefore they are all congruent.

How much do you know about translating and reflecting? Have a go at this quiz to find out!