Watch: How do you transform a shape?
This video explains how shapes can be transformed through translation, reflection or rotation.
What is reflection?

Reflection is a type of transformation. To reflect an object, you need a mirror line.
When a shape is reflected, its size does not change - the image just appears 'flipped'.
Every point on the shape is the same distance away on the other side of the mirror line.
Using squared paper can be very handy to help you reflect an object.

Example 1
Let's go through the steps to reflect a shape.
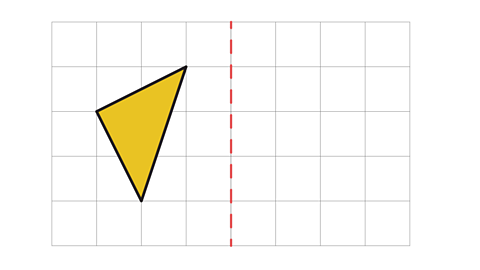
When you are reflecting a shape, you don’t need to reflect the whole shape at once.
Instead, reflect each vertex (corner) of the shape. Make sure that each vertex is the same distance away from the mirror line as the original shape.
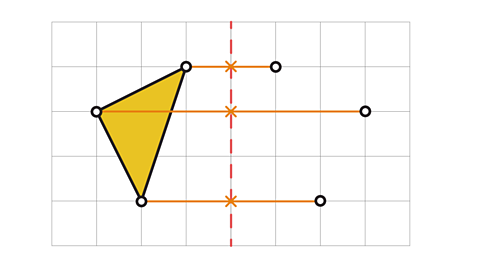
When you have plotted the reflected vertices, you join the points together again.
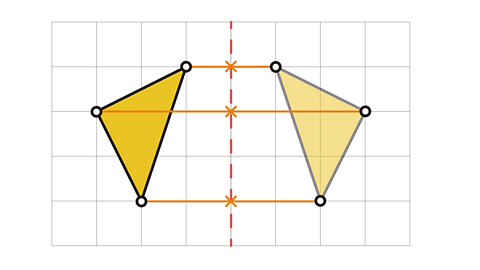
There you have your reflected shape!
Sometimes you reflect shapes in a grid. The steps to reflect the shape are exactly the same, but the reflected shape will have new coordinates.
Example 2
Let's take a look at another example:
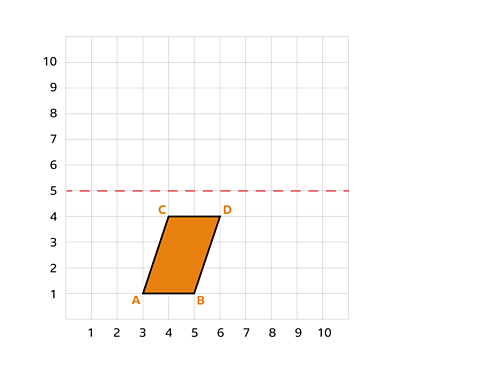
The letters represent the coordinates of the original shapes vertices.
A - (3, 1)
B - (5, 1)
C - (4, 4)
D - (6, 4)
Like before, reflect each vertex of the shape in the mirror line.
Remember to make sure that each vertex is the same amount of squares away from the mirror line as the original shape.
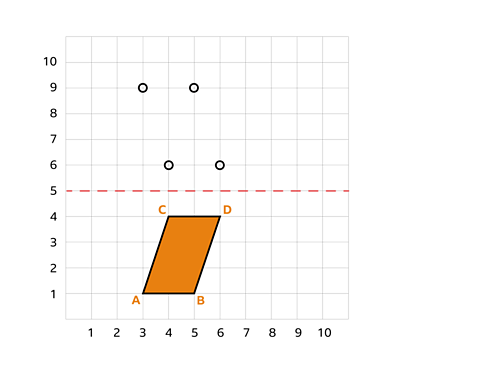
Now you have plotted the new vertices, join them to create the reflected shape.
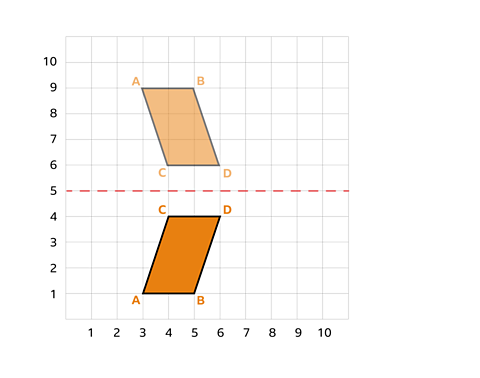
Can you see how the reflected vertices now have new coordinates?
Let’s see what they are:
| Original Coordinate | Reflected Coordinate | |
|---|---|---|
| A | (3, 1) | (3, 9) |
| B | (5, 1) | (5, 9) |
| C | (4, 4) | (4, 6) |
| D | (6, 4) | (6, 6) |
Activities
Quiz
Test your knowledge of reflection with this quiz!
Activity 2

You will need a piece of paper (ideally squared or dotted), a pencil and maybe a mirror for this activity.
Investigate which capital letters look exactly the same in each quadrant when reflected through two mirror lines
In this investigation, you are going to explore which capital letters have exactly the same reflection when reflected across two mirror lines.
'A' has been done for you below. Can you find the others?

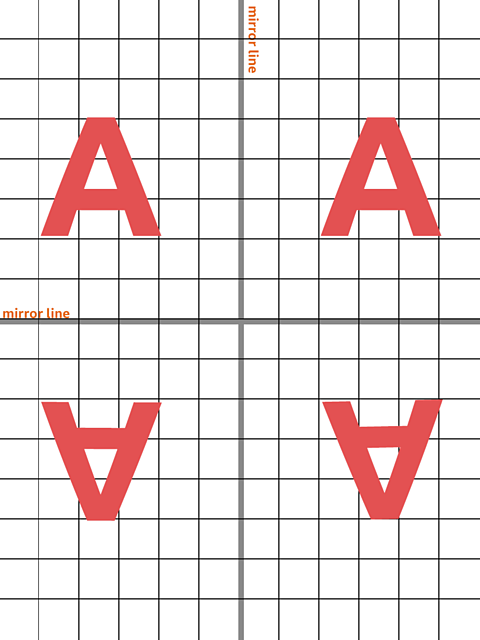

Top Tip: There are 4 letters to find!
Click for the answers.
Extension Challenge: Have a go at drawing your initials in one quadrant and then reflecting them across two different mirror lines into the other three quadrants.
NEW! Play Guardians: Defenders of Mathematica - the Halloween update. gameNEW! Play Guardians: Defenders of Mathematica - the Halloween update
Experience Mathematica as you’ve never seen it before, with all-new backgrounds and costumes for Halloween. Available for a limited time only. Use your maths skills to save the day before it's too late!

More on Position and direction
Find out more by working through a topic
- count3 of 3

- count1 of 3
